K-5 Virginia Mathematics Specialist Project: A Preliminary Report
The case study participants engaged in a range of leadership activities in their school buildings and districts. They worked regularly with teachers to deliver formal and informal professional development. They also modeled lessons, conducted grade level/vertical team meetings, orchestrated school-wide assessment procedures for mathematics or provided additional remedial support for small groups of students, and so on. Here we recount one of these activities to illustrate how they used their course experiences to support their daily work.
As the case study participants worked with students, they frequently used their understanding of mathematical ideas to make key teacher moves. In some cases these instructional moves were a result of on-the-fly decisions they made to address students' misunderstandings. In other instances, these moves were part of their regular lesson plans. In both situations, the case study participants made important pedagogical decisions based on their mathematical understandings as they supported students' learning. They developed novel ways to translate their understandings in various teacher moves to facilitate students' learning opportunities. Following Deborah Ball, we refer to these instances as situations for using mathematical knowledge for teaching.
To illustrate this point, we consider a situation that occurred as Ms. Smith worked with a small group of 5th graders who were having difficulty with fractions. (The 5th grade teachers asked her to work with these students to prepare them for the upcoming state mathematics assessment.) Ms. Smith began this session by asking the students to use pattern blocks to make a yellow hexagon shape using other pattern blocks to represent 1 unit.
As each of the students explained their pattern block configurations, they seemed confused about what each of these green triangles represented. Although some of the students indicated correctly that the green triangles represent 1/6 because there were 6 pieces, it was not clear from their explanations if they understood that these pieces needed to be the same size. To address this (unforeseen) misconception, Ms. Smith made a different shape using all 6 shapes (see picture below);
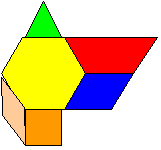
she referred to this configuration as a "funky cookie." After making the cookie, she asked the students what fraction the yellow hexagon block represented. She then asked if she could share the cookie fairly by giving each student one of the shapes that made up the cookie.
At this juncture, Ms. Smith had made a deliberate decision to alter her lesson plan to address the students' misconceptions. To address their misconceptions, she posed a different task, one that provided her students the opportunity to reason more deeply about the meaning of fractional parts. At the face of it, her decision to create the "funky cookie" was a critical point during the lesson. As a consequence of posing this new task, her students had an opportunity to develop a better understanding of those equal parts that comprise the unit. Ms. Smith applied her own understanding of fractions to facilitate her student learning. She had used one of the key mathematical ideas the underpin fractions to make an appropriate teacher move as she addressed these students' misconceptions. In this example, her decision to make a pattern block configuration that involved unequal pieces was a particularly significant move that signified her own deep understanding of key ideas.
Ms. Smith's example is representative of the quality of the types of instructional moves that we have observed as case study participants engaged in their daily work. We are convinced that they have had many opportunities over the last two years to build new understandings of the mathematics that underpins elementary school mathematics. They had developed new ways to use their understandings to engage in their work with students. In some cases, they explicitly stated this fact during our interviews. Ms. Killian, another case study participant, for instance made reference voluntarily about how the course work had changed the way in which she teaches:
During the lesson we dealt with the idea of the parts and what make up the whole (pizza)...Some of the same things we were dealing with this past summer in our own Rational Number class. Prior to taking the course last summer, I would have been right there with my students. Instead of asking my students to think about whether or not there were enough pieces to make a whole pizza, I would have said, "Okay let's multiply by two and get a common denominator"...I wouldn't have had a clue as to how to teach fractions.
As her comments indicate she attributed her questioning techniques during the lesson to her experiences in the degree program. Not only did she build her understanding of the mathematics she teaches, but also she applied these ideas as she made instructional decisions about her students' learning. One of the benefits of the mathematics specialist program is that at least for the case study teachers, as they developed and refined their understandings of the mathematics they teach, these new understandings became the basis for how they might better support student learning.
During the presentation we will offer other examples of how the mathematics specialists draw on their mathematical knowledge as the support teachers and students. We also illustrate one of the sessions during some of the courses to make more direct links between the mathematics that they explored during the courses and the mathematics that they used in their daily work.